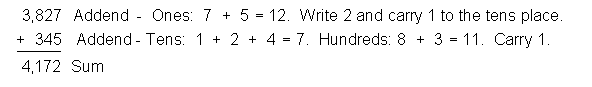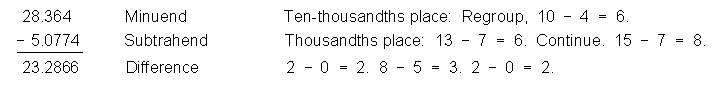Compare whole numbers
Mentally position the numbers on a number line. The leftmost number is the smaller number. Write an inequality using the less than < symbol by starting with the smaller number. Write an inequality using the greater than > symbol by starting with the larger number.
Write two inequalities comparing 4 and 7.
4 < 7
7 > 4
Locate the numbers on the number line.
The leftmost number is the smaller number. A less-than inequality starts with the smaller number.
The rightmost number is the larger number. A greater-than inequality starts with the larger number.
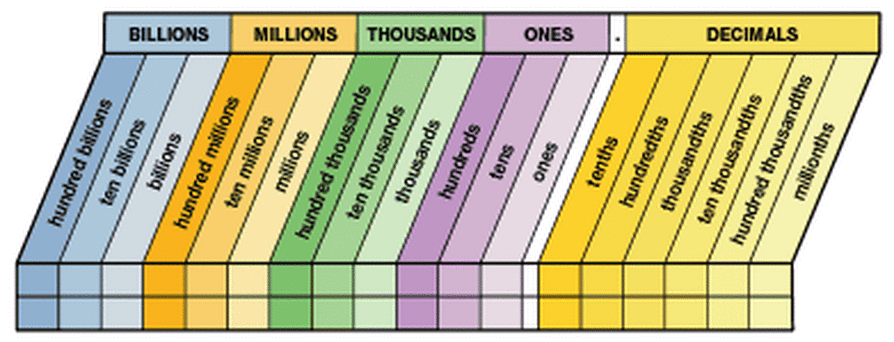
Place Value:
1) Identify the place value of 8 in the number 3,207,685,194.
2) Identify the place value of 4 in the number 3,207,685,194.
3) Identify the place value of 2 in the number 3,207,685,194.
4) In the number 4,719,680,253, identify the digit in the hundreds place.
5) In the number 4,719,680,253, identify the digit in the millions place.
6) Compare 2 and 20.
7) Compare 100 and 1
8) List these numbers in ascending order: 1101, 1011, 1001, 1100, 1010.
9) List these numbers in descending order: 2102, 2201, 2112, 2211, 2012.
10) List these numbers in ascending order: 321, 123, 213, 312, 231, 132.
Write two inequalities comparing 4 and 7.
4 < 7
7 > 4
Locate the numbers on the number line.
The leftmost number is the smaller number. A less-than inequality starts with the smaller number.
The rightmost number is the larger number. A greater-than inequality starts with the larger number.
Place Value:
1) Identify the place value of 8 in the number 3,207,685,194.
2) Identify the place value of 4 in the number 3,207,685,194.
3) Identify the place value of 2 in the number 3,207,685,194.
4) In the number 4,719,680,253, identify the digit in the hundreds place.
5) In the number 4,719,680,253, identify the digit in the millions place.
6) Compare 2 and 20.
7) Compare 100 and 1
8) List these numbers in ascending order: 1101, 1011, 1001, 1100, 1010.
9) List these numbers in descending order: 2102, 2201, 2112, 2211, 2012.
10) List these numbers in ascending order: 321, 123, 213, 312, 231, 132.
Place value
Round a whole number or a decimal number to a specified place valueWhole number:
1. Locate the rounding place. 2. Examine the digit to the right. 3. Round down by replacing digits to the right of the rounding place with zeros if the digit in the rounding place is less than 5. 4. Round up by adding 1 to the rounding place and replacing digits to the right of the rounding place with zeros if the digit in the rounding place is 5 or more. Round 5,632 to the nearest hundred. 6 is in the hundreds place; 3 is the digit to the right and 3 is less than 5. Leave the 6 as is and replace the digits in the tens and ones places with zeros. The rounded value is 5,600. Decimal number: Round as in whole numbers, but digits after the decimal to the right of the digit in the rounding place are dropped rather than replaced with zeros. Round 7.96 to the nearest tenth. 9 is in the tenths place and 6 is the digit to the right. 6 is greater than 5, so add 1 to 9, giving 10. Place the zero in the tenths place and carry the 1 to the 7 in the ones place, making it an 8. Drop the 6. The rounded value is 8.0. The zero is not dropped. This shows that the value is to the nearest tenth instead of the nearest whole. Answers:
1-b 2-c 3-b 4-a 5-b 6-d 7-b 8-a 9-c 10-d |
Classwork:
1) Which number is closest to 37.4?
a-37.407 b-37.398 c-37.3 d-37.43 2) Round 57.68 to the tens place. a-60 b-57.7 c-58 d-55 3) Round 5.968 to the tenths place. a-5.9 b-5.97 c-6.0 d-6.1 4) The Internal Revenue Service allows you to round values to the nearest dollar on your income tax return. If you entered a deduction of $513.51 rounded to the nearest dollar, what would you enter? a-$514 b-$513 c-$513.50 d-$515 5) Round $68.7589 to the nearest cent. a-$68.75 b-$68.76 c-$68.759 d-$68.80 6) Round 5.75 to one nonzero digit. a-5 b-5.8 c-6.1 d-6 7) Round 88.3 to one nonzero digit. a-90 b-88 c-80 d-100 8) Round 0.52 to one nonzero digit. a-1 b-0.6 c-0.5 d-0.52 9) You stop at the grocery store on the way home to pick up a few items. Round to one nonzero digit for items valued at $0.39, $0.45, $1.39, and $2.98. a-$0.30, $0.40, $1, $3 b-$0.40, $0.50, $1, $3 c-$0.40, $0.50, $1.40, $3 d-$0.30, $0.50, $1, $3 10) Kilowatt readings were taken for the months of June at 1,454, July at 1,703, August at 1,698, September at 1,157, and October at 983. Round each amount to the nearest thousands to identify the months with the most similar power usage. a-June 1,000; July 1,000; August 1,000; September 1,000; October 900 b-June 2,000; July 2,000; August 2,000; September 2,000; October 1,000 c-June 1; July 2; August 2; September 1; October 1 d-June 1,000; July 2,000; August 2,000; September 1,000; October 1,000 |
Add and subtract whole numbers and decimals
Addition is a binary operation that is commutative (order does not matter): a + b = b + a
3 + 6 = 6 + 3 = 9 Commutative property of addition
Addition is associative (grouping does not matter): (a + b) + c = a + (b + c)
(5 + 2) + 4 = 5 + (2 + 4) = 11 Associative property of addition
Zero property of addition (additive identity): 0 + n = n + 0 = n
0 + 5 = 5 + 0 = 5 Zero property of addition
Add whole numbers: Arrange addends in columns of like places. Add each column, beginning with the ones place. Carry (regroup) when necessary.
3 + 6 = 6 + 3 = 9 Commutative property of addition
Addition is associative (grouping does not matter): (a + b) + c = a + (b + c)
(5 + 2) + 4 = 5 + (2 + 4) = 11 Associative property of addition
Zero property of addition (additive identity): 0 + n = n + 0 = n
0 + 5 = 5 + 0 = 5 Zero property of addition
Add whole numbers: Arrange addends in columns of like places. Add each column, beginning with the ones place. Carry (regroup) when necessary.
Add decimal numbers:
Add decimal numbers by arranging the addends so that the decimal points are aligned.
Add: 34.27 + 4.3 + 0.584
Arrange addends so that the decimal points are aligned.
Add decimal numbers by arranging the addends so that the decimal points are aligned.
Add: 34.27 + 4.3 + 0.584
Arrange addends so that the decimal points are aligned.
Estimate and check addition:
Estimate by rounding the addends before finding the sum.
Check addition by adding a second time.
Estimate the sum of 528 and 867 by rounding to the nearest hundred:
528 + 867 Round each number.
500 + 900 = 1,400 Add to give approximate sum.
Exact sum is 1,395.
Subtraction is a binary operation that is neither commutative nor associative.
Addition and subtraction are inverse operations.
If 6 + 7 = 13, then 13 – 6 = 7 or 13 – 7 = 6. Inverse operations
Zero property of subtraction: n – 0 = n
8 – 0 = 8 Zero property of subtraction
Subtract whole numbers:
Arrange numbers in columns of like places.
Subtract each column beginning with the ones place.
Regroup when necessary.
Estimate by rounding the addends before finding the sum.
Check addition by adding a second time.
Estimate the sum of 528 and 867 by rounding to the nearest hundred:
528 + 867 Round each number.
500 + 900 = 1,400 Add to give approximate sum.
Exact sum is 1,395.
Subtraction is a binary operation that is neither commutative nor associative.
Addition and subtraction are inverse operations.
If 6 + 7 = 13, then 13 – 6 = 7 or 13 – 7 = 6. Inverse operations
Zero property of subtraction: n – 0 = n
8 – 0 = 8 Zero property of subtraction
Subtract whole numbers:
Arrange numbers in columns of like places.
Subtract each column beginning with the ones place.
Regroup when necessary.
Subtract decimal numbers:
Subtract decimal numbers by arranging the minuend and subtrahend so that the decimal points are aligned.
Subtract: 28.364 – 5.0774
Subtract decimal numbers by arranging the minuend and subtrahend so that the decimal points are aligned.
Subtract: 28.364 – 5.0774
Estimate subtraction:
Estimate by rounding the minuend and subtrahend before finding the difference.
Estimate the difference between 982 and 328 by rounding to the nearest hundred:
982 – 328 Round each number to hundreds.
1,000 – 300 = 700 Subtract.
Approximate difference.
Exact difference is 982 – 328 = 654.
Check subtraction:
Check subtraction by adding the difference and the subtrahend.
The result should equal the minuend.
Check the difference in the previous example
982 – 328 = 654.654 + 328 = 982 Difference + Subtrahend = Minuend
Estimate by rounding the minuend and subtrahend before finding the difference.
Estimate the difference between 982 and 328 by rounding to the nearest hundred:
982 – 328 Round each number to hundreds.
1,000 – 300 = 700 Subtract.
Approximate difference.
Exact difference is 982 – 328 = 654.
Check subtraction:
Check subtraction by adding the difference and the subtrahend.
The result should equal the minuend.
Check the difference in the previous example
982 – 328 = 654.654 + 328 = 982 Difference + Subtrahend = Minuend