Word Problems
|
|
|
Geometry Word Problems Involving PerimeterExample 1:
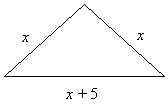
A triangle has a perimeter of 50. If 2 of its sides are equal and the third side is 5 more than the equal sides, what is the length of the third side? Solution: Step 1: Assign variables: Let x = length of the equal side Sketch the figure Step 2: Write out the formula for perimeter of triangle. P = sum of the three sides Step 3: Plug in the values from the question and from the sketch. 50 = x + x + x+ 5 Combine like terms 50 = 3x + 5 Isolate variable x 3x = 50 – 5 3x = 45 x =15 Be careful! The question requires the length of the third side. The length of third side = 15 + 5 =20 |
The following video is about writing an equation and finding the dimensions of a rectangle knowing the perimeter and some information about the about the length and width. |
Geometry Word Problems Involving AreaExample 1:
A rectangle is 4 times as long as it is wide. If the length is increased by 4 inches and the width is decreased by 1 inch, the area will be 60 square inches. What were the dimensions of the original rectangle? Solution: Step 1: Assign variables: Let x = original width of rectangle Sketch the figure Step 2: Write out the formula for area of rectangle.
A = lw Step 3: Plug in the values from the question and from the sketch. 60 = (4x + 4)(x –1) Use distributive property to remove brackets 60 = 4x2 – 4x + 4x – 4 Put in Quadratic Form 4x2 – 4 – 60 = 0 4x2 – 64 = 0 This quadratic can be rewritten as a difference of two squares (2x)2 – (8)2 = 0 Factorize difference of two squares (2x)2 – (8)2 = 0 (2x – 8)(2x + 8) = 0 We get two values for x. Since x is a dimension, it would be positive. So, we take x = 4 The question requires the dimensions of the original rectangle. The width of the original rectangle is 4. The length is 4 times the width = 4 × 4 = 16 |