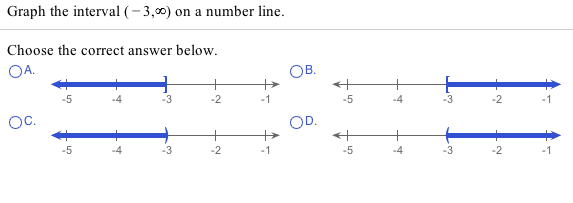
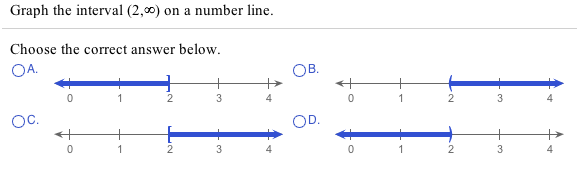
Order of Operations
|
Erin works in the mail order department of a music company. She was asked to fill the order on the right. Erin finds all of the material in stock, so she totals the order to prepare it for shipping. There is also a $4 shipping and handling charge for each order.
Erin writes: Total 3 x 6 + 5 x 12 + 4 Erin calculates $280 for the cost of the order. $280 is high for such a small order. SHe goes back to the original order to find her mistake. How did she end up with such a big number? |
Order to Fill:
|
New Idea:
There is a special order that must be followed when solving problems with more than one operation. Multiplication and division must be done before addition and subtraction. The order is called the order of operations.
Erin should have multiplied before she added. Step 1: Multiply first. Step 2: Add 3 x 6 + 5 x 12 + 4 = 82 So the total price is $82. When a problem has only addition and subtraction, work from left to right. Example: Find the value of 16 - 9 + 3 Subtract 16 - 9 Add 7 + 3 = 10 Always multiply and divide from left to right before adding or subtracting. Example: Find the value of 36 - 16 / 2 x 4 + 5 Step 1: Multiply and divide from left to right. Divide first Step 2: Multiply Step 3: Add and subtract from left to right. Subtract first Step 4: Add 36 - 16 / 2 x 4 + 5 |
3 x 6 + 5 x 12 + 4 = 82
18 + 60 + 4 = 82 36 - 16 / 2 x 4 + 5 36 - 8 x 4 + 5 36 - 8 x 4 + 5 36 - 32 + 5 36 - 32 + 5 4 + 5 = 9 |
Remember: Some calculators follow the order of operations. Some don't.
Order of Operations
Using the Correct Order of Operations
We are going to continue our lesson on order of operations and you will be able to evaluate expressions using the correct order of operations.
|
|
Why do two negative numbers make a positive number
Some people think of negative as meaning "not." So if I say "I am not going to the store," that is sort of the negative version of "I am going to the store." So what do two "nots" mean? Consider this sentence: "You may tell me NOT to go to the store, but I'm NOT going to do what you say!" By negating your negation, I am insisting that I WILL go to the store.
OK, you get the idea? Two "nots" cancel each other out, just like two negatives. That was the appetizer: here comes the main course...
Another way to look at it
One way to think of numbers is in terms of money. Let's say you and I are playing poker. To make life convenient, we use chips instead of real money. A green chip is worth $5. A red chip means that you owe $5. So if you lose $5, you can represent that by giving up a green chip, or (if you're out) by picking up a red chip. Of course, you are always allowed to pick up a green chip and a red chip at the same time, because that doesn't change your total sum. (At the end, presumably, we'll cash in all our chips and see who gains or loses what money.) I hope you see the mathematical analogy I'm drawing here: A green chip represents +$5, and a red chip represents -$5. Make sense? If so, here comes multiplication in terms of chips.
If you gain three green chips, what happens? Intuitively, you know that you gain $15. Mathematically, we take the +$5 that one chip is worth, and multiply it by +3, to indicate that you are gaining three chips. 3 x $5 = $15; positive times positive is positive.
If you gain three red chips, what happens? If you think about it, I think you'll agree that you just lost $15. Mathematically, this looks the same as the previous example, except that the +$5 that represents a green chip, is replaced by -$5 to represent a red chip. 3 x -$5 = -$15; positive times negative is negative.
Now, what if you lose three green chips? Once again, you have lost $15. We represent this "loss" mathematically by changing the 3 into a -3, so our equation is: -3 x $5 = -$15. Negative times positive is negative.
And finally, what if you lose three red chips? Hooray! This is happy news, it means you have actually gained money. Mathematically, this is -3 (since you lost) times -$5 (since they were red chips). -3 x -$5 = +$15. Negative times negative is positive.
A third way to look at it
Another way to think about negative numbers is that they "continue the sequence" as positive numbers go down. In other words, if I go from 4 to 3 to 2 to 1 to 0 and then keep going, I get into the negative numbers. Nothing should change drastically when I make that switch. So, consider what happens when I take all the numbers in that sequence, and multiply them by 5:
4 x 5 = 20
3 x 5 = 15
2 x 5 = 10
1 x 5 = 5
0 x 5 = 0
What's happening on the left is that the numbers are going down by one. What's happening on the right is that the numbers are going down by 5.
If we keep dropping the left-hand column by one, we expect the trend to continue. Hence, the next few terms are...
-1 x 5 = -5
-2 x 5 = -10
-3 x 5 = -15
...and so on. So this tells us that a negative times a positive is a negative.
Now, let's do the same thing with the multiples of -5 instead of 5.
4 x -5 = -20
3 x -5 = -15
2 x -5 = -10
1 x -5 = -5
0 x -5 = 0
Once again, on the left, our terms are going down by 1. But what's happening on the right? The terms are going up by 5 each time. (If you don't believe this, think of them as temperatures. When you go from -20 to -15, the temperature has gone up by 5.) So if that sequence continues, we will see...
-1 x -5 = 5
-2 x -5 = 10
-3 x -5 = 15
Once again, a negative times a negative is a positive.
This method doesn't have the punchy mnemonic quality of the first answer, or the rigor of the fourth. And it doesn't convey powerful intuition as well as the second answer, which is my favorite. But it does have this benefit: if you start to think about negative numbers this way, as what happens to positive numbers when you count down, you can also answer other questions such as "What do negative exponents mean?" (In other words, what is 5-3?)
a fourth way of looking at it
Finally, for people who like algebraic sorts of proofs, consider this. A and B are both positive numbers. I will start with a statement that is definitely true, and then I will multiply both sides by B. A + (-A) = 0
(A)(B) + (-A)(B) = 0
Since the term on the left is positive, the term on the right must be negative. (I'm assuming here that if two non-zero numbers add up to zero, then one of them is negative and one is positive—I think that is too obvious to require a proof.) This proves that negative times positive is negative. Now:
A + (-A) = 0
(A)(-B) + (-A)(-B) = 0
Since the term on the left is negative (as we just proved!), the term on the right must be positive.
OK, you get the idea? Two "nots" cancel each other out, just like two negatives. That was the appetizer: here comes the main course...
Another way to look at it
One way to think of numbers is in terms of money. Let's say you and I are playing poker. To make life convenient, we use chips instead of real money. A green chip is worth $5. A red chip means that you owe $5. So if you lose $5, you can represent that by giving up a green chip, or (if you're out) by picking up a red chip. Of course, you are always allowed to pick up a green chip and a red chip at the same time, because that doesn't change your total sum. (At the end, presumably, we'll cash in all our chips and see who gains or loses what money.) I hope you see the mathematical analogy I'm drawing here: A green chip represents +$5, and a red chip represents -$5. Make sense? If so, here comes multiplication in terms of chips.
If you gain three green chips, what happens? Intuitively, you know that you gain $15. Mathematically, we take the +$5 that one chip is worth, and multiply it by +3, to indicate that you are gaining three chips. 3 x $5 = $15; positive times positive is positive.
If you gain three red chips, what happens? If you think about it, I think you'll agree that you just lost $15. Mathematically, this looks the same as the previous example, except that the +$5 that represents a green chip, is replaced by -$5 to represent a red chip. 3 x -$5 = -$15; positive times negative is negative.
Now, what if you lose three green chips? Once again, you have lost $15. We represent this "loss" mathematically by changing the 3 into a -3, so our equation is: -3 x $5 = -$15. Negative times positive is negative.
And finally, what if you lose three red chips? Hooray! This is happy news, it means you have actually gained money. Mathematically, this is -3 (since you lost) times -$5 (since they were red chips). -3 x -$5 = +$15. Negative times negative is positive.
A third way to look at it
Another way to think about negative numbers is that they "continue the sequence" as positive numbers go down. In other words, if I go from 4 to 3 to 2 to 1 to 0 and then keep going, I get into the negative numbers. Nothing should change drastically when I make that switch. So, consider what happens when I take all the numbers in that sequence, and multiply them by 5:
4 x 5 = 20
3 x 5 = 15
2 x 5 = 10
1 x 5 = 5
0 x 5 = 0
What's happening on the left is that the numbers are going down by one. What's happening on the right is that the numbers are going down by 5.
If we keep dropping the left-hand column by one, we expect the trend to continue. Hence, the next few terms are...
-1 x 5 = -5
-2 x 5 = -10
-3 x 5 = -15
...and so on. So this tells us that a negative times a positive is a negative.
Now, let's do the same thing with the multiples of -5 instead of 5.
4 x -5 = -20
3 x -5 = -15
2 x -5 = -10
1 x -5 = -5
0 x -5 = 0
Once again, on the left, our terms are going down by 1. But what's happening on the right? The terms are going up by 5 each time. (If you don't believe this, think of them as temperatures. When you go from -20 to -15, the temperature has gone up by 5.) So if that sequence continues, we will see...
-1 x -5 = 5
-2 x -5 = 10
-3 x -5 = 15
Once again, a negative times a negative is a positive.
This method doesn't have the punchy mnemonic quality of the first answer, or the rigor of the fourth. And it doesn't convey powerful intuition as well as the second answer, which is my favorite. But it does have this benefit: if you start to think about negative numbers this way, as what happens to positive numbers when you count down, you can also answer other questions such as "What do negative exponents mean?" (In other words, what is 5-3?)
a fourth way of looking at it
Finally, for people who like algebraic sorts of proofs, consider this. A and B are both positive numbers. I will start with a statement that is definitely true, and then I will multiply both sides by B. A + (-A) = 0
(A)(B) + (-A)(B) = 0
Since the term on the left is positive, the term on the right must be negative. (I'm assuming here that if two non-zero numbers add up to zero, then one of them is negative and one is positive—I think that is too obvious to require a proof.) This proves that negative times positive is negative. Now:
A + (-A) = 0
(A)(-B) + (-A)(-B) = 0
Since the term on the left is negative (as we just proved!), the term on the right must be positive.
Order of Operations:
Today we are going to learn about the 'Order of Operations'.
Numbers and operation signs are used to write expressions.
You simplify an expression when you perform the operations.
When there is more than one operation, you must follow the Order of Operations.
First, multiply and divide from left to right.
Then, add and subtract from left to right.
Simplify 16 - 6 x 2
What do you do first?
Multiply first. 6 x 2 = 12
Then you will subtract 16 - 12 = 4
The value of 16 - 6 x 2 = 4.
Would you come up with a different answer if you tried to solve the equation in a different order?
Try this: 16 - 6
What is the solution to this equation?
16 - 6 = 10
Now lets finish the equation: 10 x 2 = 20
When we followed a different order, we came up with a different answer.
Therefore, it is important to follow the order of operations to find the correct solution.
Numbers and operation signs are used to write expressions.
You simplify an expression when you perform the operations.
When there is more than one operation, you must follow the Order of Operations.
First, multiply and divide from left to right.
Then, add and subtract from left to right.
Simplify 16 - 6 x 2
What do you do first?
Multiply first. 6 x 2 = 12
Then you will subtract 16 - 12 = 4
The value of 16 - 6 x 2 = 4.
Would you come up with a different answer if you tried to solve the equation in a different order?
Try this: 16 - 6
What is the solution to this equation?
16 - 6 = 10
Now lets finish the equation: 10 x 2 = 20
When we followed a different order, we came up with a different answer.
Therefore, it is important to follow the order of operations to find the correct solution.
Order of Operations
Rules that tell you which operations to do first.
Terms
Parts of an expression that is separated by an addition (+) or subtraction (-) sign.
Like Terms
Terms that have the same variables with the same exponents.
Coefficient
A number that multiplies a variable.
Associative Property
The grouping of more than two numbers that does not matter when you add or multiply.
Zero Property of Multiplication
The product of any number and 0 is 0.
|
Variable
A letter that represents a number.
Constants
A constant is a number of variable that does not change.
Substitute
Replace a variable with a number or an expression.
Equation
A statement that two expressions are equal.
Identity Property
Adding 0 or multiplying by 1, does not change the number.
Addition Property of Opposites
The sum of a number and its opposite is 0.
Distributive Property
Multiply a sum or difference by a number by multiplying each term of the sum or difference by the number.
|
Let's solve the aforementioned equations:
Write the following equations on a piece of paper that you will turn in at the end of class.
|
|
Discuss with your Partner
Take a moment to turn to your partner and explain how you solved question 16.
Now work with your partner and solve the following equation:
9 x 5 / 15 - 3
Now work with your partner and solve the following equation:
9 x 5 / 15 - 3
Grouping Symbols
Sometimes expressions contain parentheses. Be sure to do these operations inside the parentheses first.
|
Simplify the following:
4 x ( 7 - 3) Do the parentheses first. (7 - 3) 7 - 3 = 4 Then multiply. 4 x 4 = 16
|
Simplify the following:
( 4 + 5) / 3 x 3 What are you going to do first? Simplify: - (3 - 8) - 9 Do the subtraction in the parentheses first.
|
Discuss with your partner:
Listen while a partner explains how to simplify the expression in number 13 above. Follow the steps as your partner explains.
Now simplify 6 - 4 / 2. Have your partner simplify ( 6 - 4 ) / 2
Compare your answers. Are they different? Why?
Now simplify 6 - 4 / 2. Have your partner simplify ( 6 - 4 ) / 2
Compare your answers. Are they different? Why?
Variable Expressions
A variable is a letter that stands for a number. Any letter can stand for any number. The letter t could be used to stand for a time like four hours.
You can write expressions with variables, operations, and numbers.
You can write expressions with variables, operations, and numbers.
|
Example:
What does xy mean? x ___ y xy means x times y |
1) What does 3y mean?
2) k/4 means k ____ 4 3) 4b - 3 means 4 ___ b ____ 3 4) 2d + 9 means 2 ___ d ___ 9 5) -8n + 3 means -8 ___ n ___ 3 |
Work with your partner
Write a variable expression using addition and multiplication. Have your partner solve it. Check their work.