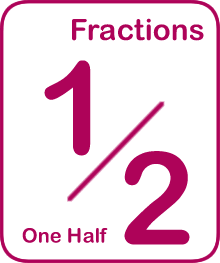Fractions

By the end of the lesson you will be able to:

What is a Prime Factor?

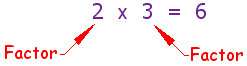
A factor that is a prime number. One of the prime numbers that, when multiplied, give the original number.

Example: The prime factors of 15 are 3 and 5 (3×5=15, and 3 and 5 are prime numbers).

What is a Factor?

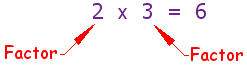
"Factors" are the numbers you multiply together to get another number:

What is Prime Factorization?

"Prime Factorization" is finding which prime numbers multiply together to make the original number.

Example:

What are the prime factors of 12 ? It is best to start working from the smallest prime number, which is 2, so let's check:

12 ÷ 2 = 6

Yes, it divided evenly by 2. We have taken the first step!

But 6 is not a prime number, so we need to go further. Let's try 2 again:

6 ÷ 2 = 3

Yes, that worked also. And 3 is a prime number, so we have the answer:

12 = 2 × 2 × 3

As you can see, every factor is a prime number, so the answer must be right.

Note: 12 = 2 × 2 × 3 can also be written using exponents as 12 = 22 × 3

What is a Fraction?

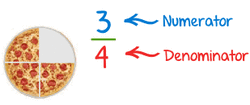
Part of a whole.

A number written with the bottom part (the denominator) telling you how many parts the whole is divided into, and the top part (the numerator) telling how many you have.

Numerator

The numerator is the top number of a fraction.
This is the number of parts in a whole.

Denominator

The denominator is the bottom number in a fraction.
This is the number that represents the number of equal parts of a whole.

Fraction Lesson

Least Common Multiple Tool

What is a Multiple?

The multiples of a number are what you get when you multiply it by other numbers (such as if you multiply it by 1,2,3,4,5, etc). Just like the multiplication table.

The multiples of 3 are: 3, 6, 9, 12, 15, 18, 21, etc ... The multiples of 12 are: 12, 24, 36, 48, 60, 72, etc...

What are Common Multiples?

When you list the multiples of two (or more) numbers, and find the same value in both lists, then that is a common multiple of those numbers.

For example, when you write down the multiples of 4 and 5, the common multiples are those that are found in both lists:

The multiples of 4 are: 4,8,12,16,20,24,28,32,36,40,44,...

The multiples of 5 are: 5,10,15,20,25,30,35,40,45,50,...

Notice that 20 and 40 appear in both lists?

So, the common multiples of 4 and 5 are: 20, 40, (and 60, 80, etc ..., too)

What is the Least Common Multiple?

It is simply the smallest of the common multiples.

In our previous example, the smallest of the common multiples is 20 ...

... so the Least Common Multiple of 4 and 5 is 20.

How do I find the Least Common Multiple?

It is a really easy thing to do. Just start listing the multiples of the numbers until you get a match.

Example: Find the least common multiple for 3 and 5:
The multiples of 3 are 3, 6, 9, 12, 15, ...,
and the multiples of 5 are 5, 10, 15, 20, ...,
like this:

As you can see on this number line, the first time the multiples match up is 15. Answer: 15