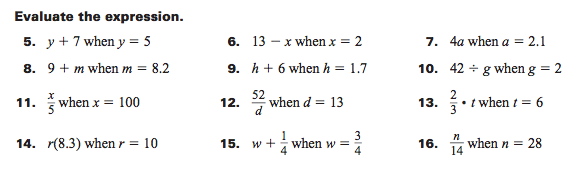Create and Evaluate Algebraic Expressions
You will be able to write and evaluate simple algebraic expressions by the end of this lesson.
Vocabulary:Order of Operations
The rules of which calculation comes first in an expression
They are: . do everything inside parentheses first: () . then do exponents, like x2 . then do multiplies and divides from left to right . lastly do the adds and subtracts from left to right Example: 5 × (3 + 4) - 2 × 8 = 5 × 7 - 2 × 8 = 35 - 16 = 19 Value
Money: how much something is worth.
Example: the value of this coin is one dollar. Mathematics: the result of a calculation. Example: 3 × 4 gives the value of 12. Equation
An equation says that two things are the same, using mathematical symbols.
An equal sign (=) is used Example: 7+2 = 10-1 |
Substitute:In Algebra "Substitution" means putting numbers where the letters are:
Example: If x=5, then what is x + 10/x ? Put "5" where "x" is: 5 + 10/5 = 7 Evaluate:To calculate the value of.
Example: Evaluate the cost of each pie if 3 pies cost $6. Answer: $2 each. solve
ExpressionNumbers, symbols and operators (such as + and ×) grouped together that show the value of something.
Example 2×3 is an expression Constant
A fixed value. In Algebra, a constant is a number on its own, or sometimes a letter such as a, b or c to stand for a fixed number. Example: in "x + 5 = 9", 5 and 9 are constants If it is not a constant it is called a variable. |
Operation
A mathematical process. The most common are add, subtract, multiply and divide (+, -, ×, ÷ ). But there are many more, such as squaring, square root, etc. If it isn't a number it is probably an operation. Example: In 25 + 6 = 9, the operation is add Variables:
A symbol for a number we don't know yet. It is usually a letter like x or y.
Example: in x + 2 = 6, x is the variable If it is not a variable it is called a Constant |
Classify Algebraic Expressions
|
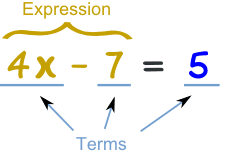
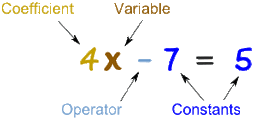
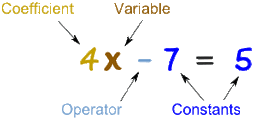
An Algebraic Expression consists of arithmetic numbers (numeral coefficients) and literal numbers (letters or variables) combined by addition, subtraction, multiplication or division. Each part of an expression and the sign before it is called a term. Terms are separated by positive/addition and negative/subtraction signs.
Binomial
A polynomial with two terms such as 4x - 7
Trinomial
A polynomial with three terms such as 3x^2 - 4x + 2
Degree of a Polynomial
The same as that of the term of greatest degree.
Polynomial
Many terms
Poly - Many -nomial may derive from Greek nomos, "law", influenced by Latin nomen, "name" |
Monomials
The following expressions are monomials:
-2 y 5w 0 -7x^2 The following expressions are not monomials: 5x + y 2 + x + z 6x^3 - 9 The non-variable factor of a monomial is called the numerical coefficient. A monomial like -3 or 25 has no variable factor and is called a constant. The degree of a monomial in a variable is the number of times the variable is a factor in the monomial. |
Name the operation indicated by the expression
1. 19x
2. 5 - b 3. 14 / m 4. 8 + 24 |
|
|
Jackson was given the expression 2x + 4 and was told to evaluate it when x = 5. Jackson did not know what to do. Explain in your own words what Jackson needs to do. Please use at least three sentences.
|